How do I analyze the symmetry?
The horse’s symmetry is calculated while trotting on a straight line: it’s the comparison between the half strides.
In our analysis, we are going to compare the vertical acceleration of the 2 half strides. Let’s have a look at some examples: below, two strides at the trot of a symmetrical horse seen in acceleration.
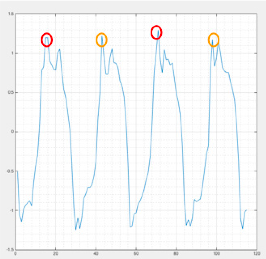
You can see the 4 series of land – support (half strides). If we compare the orange diagonal with the red diagonal, the acceleration values at the moment of landing are all basically identical. This horse is symmetrical.

For this horse, the orange diagonal is systematically weaker than the red diagonal. This horse is therefore asymmetrical.
If a horse is asymmetrical, it means that one of his two diagonals “pushes” less than the other.
After the analysis of your raw data, we give you a symmetry rating on a scale of 0 to 10. This allows you to situate your horse in relation to a perfect horse. Note that for animals, as for humans, perfect symmetry does not exist (10/10 does not exist).
In your session report, you have your symmetry rating as well as an image of your horse’s 4 hooves. They are displayed in colors corresponding to the obtained rating:
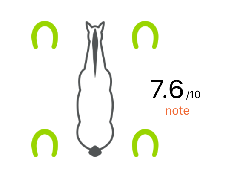
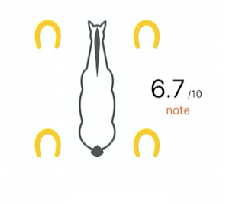
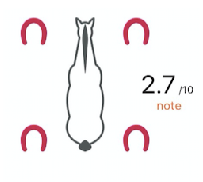
The symmetry of your horse’s gaits may vary from one training session to another without actually being a sign of lameness. Therefore, it is also necessary to compare the changes in symmetry shown by the app with the feeling you actually have while riding.
